GATE CSE 2024 | Set 1 | Question: 22

Question

Let $A$ and $B$ be non-empty finite sets such that there exist one-to-one and onto functions $\text{(i)}$ from $A$ to $B$ and $\text{(ii)}$ from $A \times A$ to $A \cup B$. The number of possible values of $\text{|A|}$ is ___________.

Answer 1

Given non-empty finite sets A & B i.e. |A| $\neq$ 0, |B| $\neq$ 0.

There exists one-to-one & onto function from A to B(A $\rightarrow$ B) and from A x A to A $\cup$ B.

Means, there exists Bijective function from A to B(A $\rightarrow$ B) and from A x A to A $\cup$ B.

 

---

IMPORTANT NOTE : If Bijective function is possible from X $\rightarrow$ Y then |A| = |B|.

---

 

Case 1 : |A|=1 : A={a} and B = {a}.

We can take A & B as equal set because question doesn't says two sets A & B should be distinct.

Function A $\rightarrow$ B :

 

|A| = |B|

It is one-to-one and onto. Hence Bijection is possible.

Now, 

A x A = { (a,a) }

A $\cup$ B = {a}

 

|A x A| = |A $\cup$ B|

Hence Bijection is possible from A x A to A $\cup$ B

So, |A| =1 is possible.

 

Case 2 : |A|=2 : A={a,b} and B = {A,B}

Function A $\rightarrow$ B :

 

|A| = |B|

It is one-to-one and onto. Hence Bijection possible.

Now, 

A x A = { (a,a), (a,b), (b,a), (b,b) }

A $\cup$ B = {a, b, A, B}

|A x A| = |A $\cup$ B|

Hence Bijection is possible from A x A to A $\cup$ B

So, |A| =2 is possible.

 

Case 3 : |A|=3 : A={a, b, c} and B = {A, B, C}

Function A $\rightarrow$ B :

 

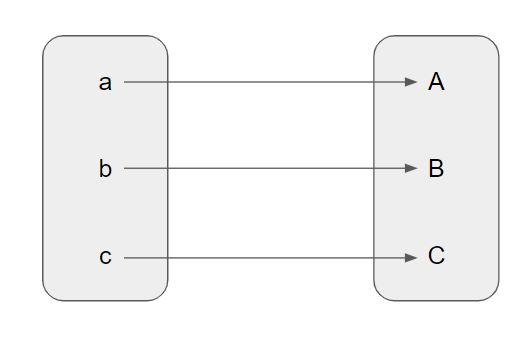
|A| = |B|

It is one-to-one and onto. Hence Bijection possible.

Now, 

A x A = { (a,a), (a,b), (a,c), (b,a), (b,b), (b,c), (c,a), (c,b), (c,c) }

A $\cup$ B = {a, b, c, A, B, C}.

Here, we can see that |A x A| $\neq$ |A $\cup$ B| (9 $\neq$ 6 ). So, Bijection is not possbile at all.

So, |A| = 3 is not possible.

---

 

|A| = 1 or 2.

So, Only 2 values are possible for |A|.

Answer : 2

Answer 2

There exist one-to-one and onto function between X and Y implies $|X| = |Y|$.

Hence, $|A| = |B|$ and $|A|^2 = |A| + |B| - |A \cap B|$.

Can $|A| = 1$?

Yes, when $|A| = |B| = |A \cap B| = 1$.

Can $|A| = 2$?

Yes, when $|A| = |B| = 2, |A \cap B| = 0$.

For larger values of $|A|$, $|A|^2 > |A| + |B|$.

Therefore, only 2 values are possible for $|A|$.